空気の力で機械を動かすのが、”空圧機器”です。 空圧機器はその使い勝手の良さから、様々な分野の機械で使用されています。 身近な例で言えば、電車のドアや歯医者さんのドリルなども空気の力で動いています。 本ブログの過去記事では、空気圧の基礎の基礎や空圧回路の設計方法を紹介しました。
さて、今回のテーマは空圧機器を取り扱う上で知っておいた方が良い理論です。 今まで説明を避けてきた数式の部分ですね。

なんだか難しそう・・・
理論と聞くと、そう感じる人も少なくないかもしれません。 でも心配いりません、どれも中学・高校で習ったレベルのものばかりですし、概要を掴むだけならそこまで難しくありません。 わかりやすく説明していきますので、気負わずに読み進めてくださいね。 ちなみに・・・あなたは下記の質問に答えられますか?
・絶対圧とゲージ圧の違いって何?
・ボイルシャルルの法則って、どういう法則?
・パスカルの原理って、どういうこと?
・連続の法則の意味を説明できる?
・ベルヌーイの定理ってどんな定理?
もし、あなたが機械設計者であり、これらの質問に一つでも答えられなければ、結構やばいかも!? 設計者ではなくても、空圧機器を利用している人であれば理解しておきたいところです。 本記事を読めば、上記の質問にフワッと答えられるようになりますよ!
では、早速いきましょう!!
圧縮空気と圧力の話
空圧機器は”圧縮空気”を利用して動作します。 圧縮空気とは、読んで字の如く、圧縮された空気のことです。 専用のコンプレッサなどを利用して、空気をギュッと圧縮することで作られます。 圧縮された空気はどうなるのかというと、"圧力"が高まります。 空圧機器では、空気を圧縮することで高まった圧力を利用するして様々な機器を動かしています。 では、そもそも圧力とは一体何なのでしょうか。
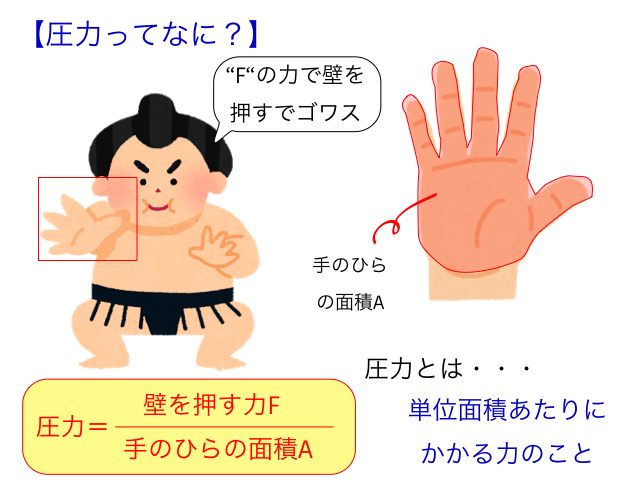
定義としては、圧力は単位面積あたりにかかる力のことを指します。 定義だけだとパッとイメージしにくいでので、一つ例を挙げます。 手で壁を押した時をイメージしてください。その時、手と壁の間に働くのが圧力です。 この時の圧力は“壁を押す力 / 壁に触れている面積“で表すことができます。 圧縮空気も手で壁を押すのと同じように、触れている面を押す力・・・すなわち"圧力"を持っています。 この圧力を利用して、あれこれ動かしてやろうぜというのが空圧機器の原理です。
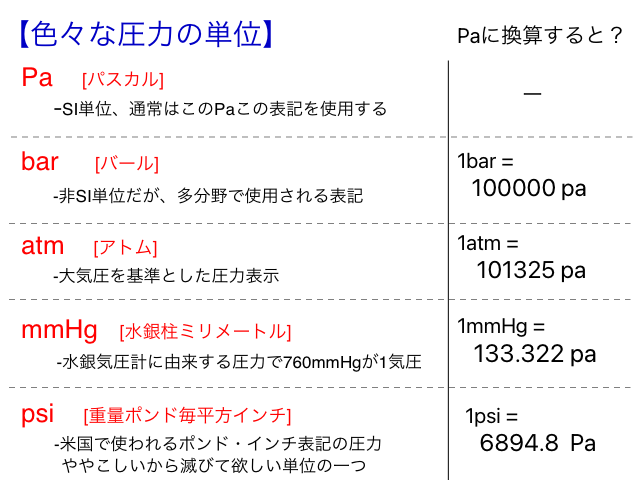
圧力の単位はPa(パスカル)で表す規定となってます。 1 [Pa]は 1 [N/m^2]とも表すことができます。 その他の圧力単位もありますので、下記の表を頭の片隅に置いておくと混乱せず便利ですよ。 換算数値は特に覚える必要はありませんよ、ネット上にいくらでも変換ツールが転がってますので。こういう単位があるんだなーくらいの認識でOKです。
空気圧の圧力の表し方には、絶対圧とゲージ圧の二つがあります。 絶対圧は、絶対真空を0として表した圧力です。 絶対真空とは、物質が全く存在しない空間で、これ以上、圧力が低くならないという理想的な状態です。 現実にはあり得ない状態ですが、ここを0として、圧力を数えるのが絶対圧です。 一方、ゲージ圧は、大気圧を0として表した圧力です。 大気圧の値は学校で習うのでご存知だと思いますが、1013hpa(ヘクトパスカル)です。 つまり、絶対圧とゲージ圧の関係は、下記のようになるわけです。
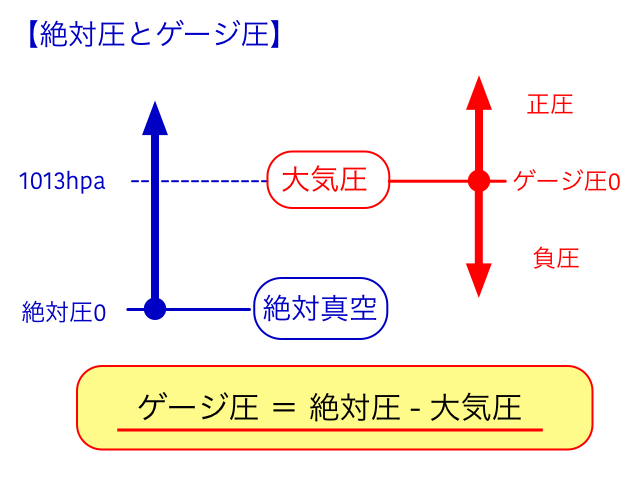
一般的に、圧力を表す際はこのゲージ圧が使用されます。覚えておきましょう。
ボイルシャルルの法則
気体の温度が上がったら空気が膨張するってイメージは、何となく直感的に分かりますよね。 ボイルシャルルの法則はこういった気体の温度・体積・圧力の関係を表した式です。 この式を理解すれば、気体の温度・体積・圧力を計算できるようになります。 おそらく、高校の物理で習っているはずですよ。
ボイル・シャルルの法則はボイルの法則、シャルルの法則の2つの法則から成り立ちます。
まず、ボイルの法則ですが、温度が変化しない条件の下では、気体の体積が圧力に反比例するこというものです。
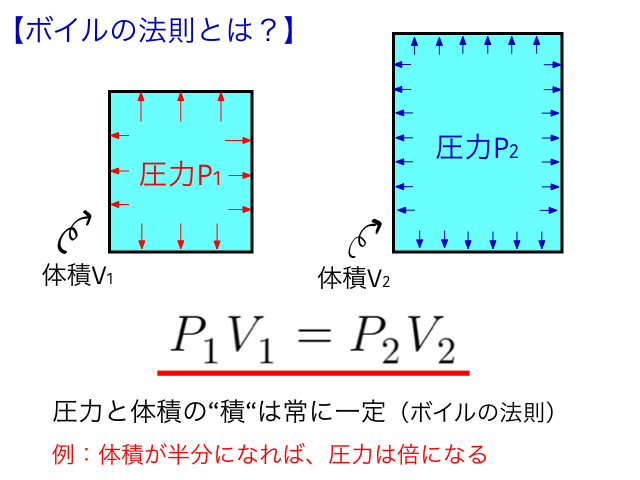
つまり
体積が半分になれば、圧力は倍になる
体積が3倍になれば、圧力は1/3になる
といった具合です。Pを圧力、Vを体積とすれば、その積のPxVは常に一定です。
次にシャルルの法則ですが 、圧力が変化しない条件の下では、気体の体積の温度変化に比例するというものです。
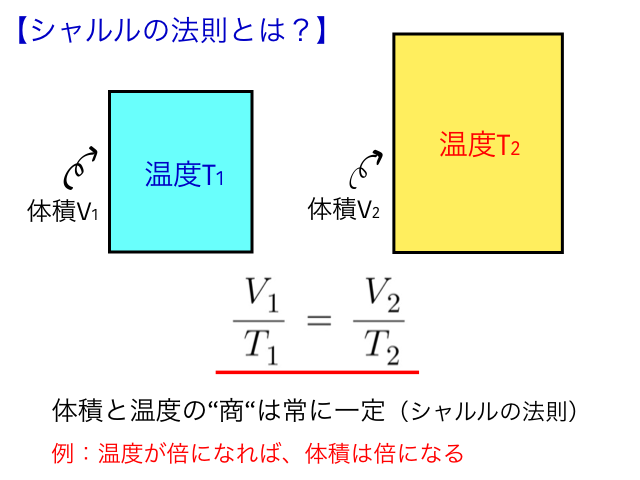
つまり
温度が倍になれば、体積は倍になる
温度が半分になれば、体積は半分になる
といった具合です。Tを温度、Vを体積とすれば、その商のV/Tは常に一定です。 この時、温度Tは我々が通常使用している[℃]ではなく、絶対温度[K]を使用するので注意しましょう。 そして、この二つの法則を合わせたのが、ボイル・シャルルの法則です。
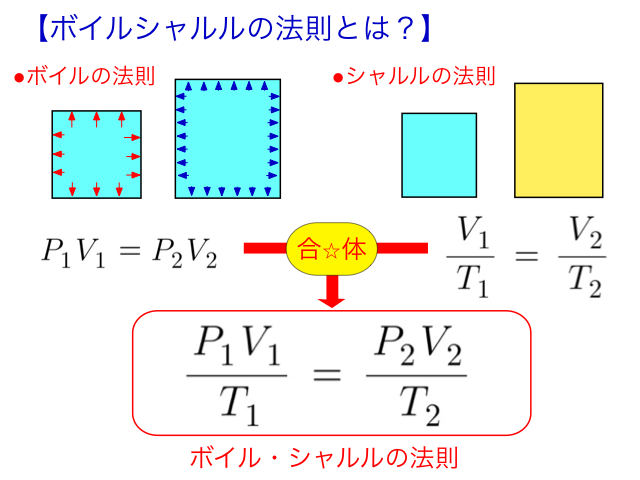
簡単な演習問題を解いて理解を深めましょう。
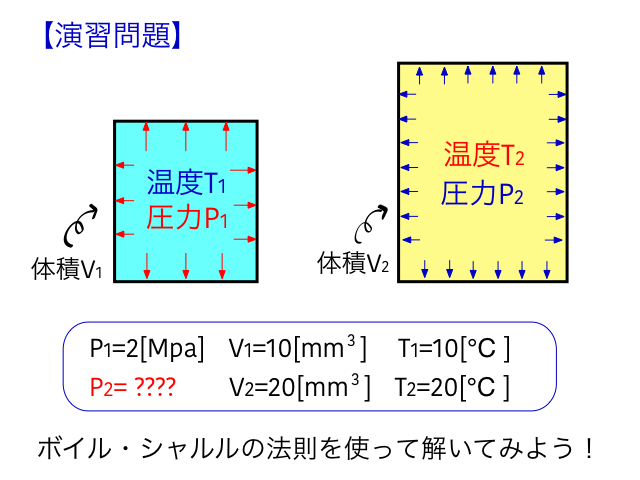
求めたいのはP2なので、式を変形します。
$$ P_2=\frac{T_2 V_1}{T_1 V_2}\ P_1 $$
この式に数字を代入していきましょう。
$$ P_2=\frac{(20+273) * 10}{(10+273) * 20}\ * 2 =1.04 [Mpa] $$
となります。温度は絶対温度で計算する必要があるのでこの点は注意です。
【ちょっと一言】
厳密に言えばボイル・シャルルの法則の考え方が成立つのは"理想気体"に対してです。 理想気体とは、計算するのに不都合となる点を無視した都合の良い気体のことでこの世の中には実在しません。 え?それじゃ結局使えないじゃん。 と思うかもしれませんが、あくまでも厳密に言えばの話なので 空圧機器が使用される条件下であれば細かいことは気にせずにこの式を使えば良いでしょう。 細かいことを言い出すとキリがないので、まずはシンプルに考えましょうということですね。
パスカルの原理
パスカルの原理は、密閉された容器の中ではあらゆる地点の圧力は等しくなるという原理です。 先ほども説明しましたが、単位面積あたりにかかる力のことを圧力といいます。では、圧力をもつ流体が容器に閉じ込められるとどうなると思いますか?
炭酸飲料のペットボトルの例で考えてみましょう。
コーラでも三ツ矢サイダーでも良いですが、炭酸飲料のペットボトルを振るとカッチカチになりますよね。これは、振った衝撃でジュースに溶けている二酸化炭素の分子が気体に戻り、ペットボトル内部の圧力を高めているんです。圧力の高まったペットボトルを触った時、どこも均等にカチカチなことがわかるはずです。どこか一部だけ柔らかいなんてことはあり得ません。これがまさにパスカルの原理であり、密閉されたペットボトル内でどの地点の圧力も均等に高くなるので全体がカチカチになるというわけです。

パスカルの原理を利用すると、流体から大きな力を取り出すことができます。
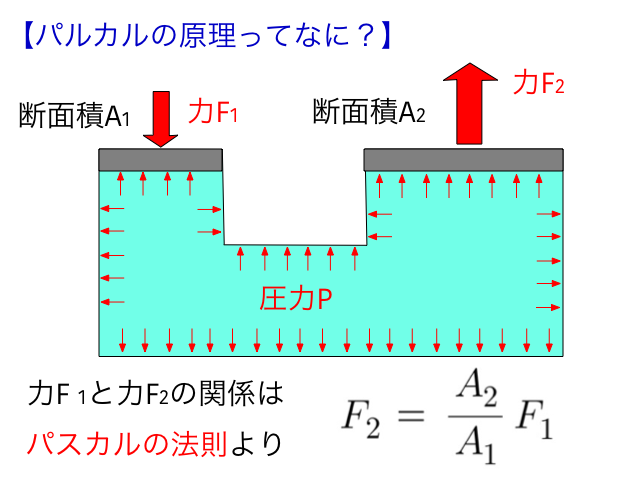
上図の小さい蓋に対してF1という力がかかっている時、容器内の圧力PはF1/A1となります。パスカルの原理では容器内のすべての箇所の圧力は一定ですから、大きい蓋にも同じ圧力が掛かります。大きい蓋の面積はA2ですから、蓋を押す力F2は圧力P x A2となります。PはF1/A1でもあるため、これを代入すると上図の関係式が導出できるわけです。つまり、断面積の比で力を増幅することができるわけです。少ない力であっても、面積の比さえ大きくすれば大きな力を取り出すことができるんです。
簡単な演習問題を解いて理解を深めましょう。
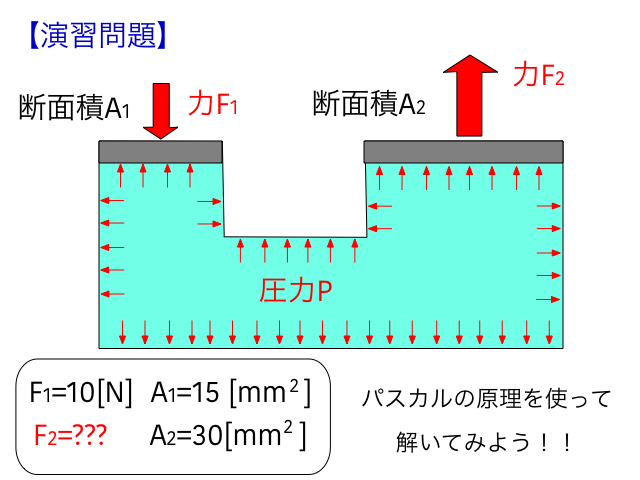
求めたいのはF2なので、式は下記のようになります。
$$F_2=\frac{A_2}{A_1}\ F_1$$
この式に数字を代入していきましょう。
$$F_2=\frac{30}{15}\ 10 = 20 [N]$$
となります。 簡単ですね。力が倍になりました!!
連続の法則
連続の法則は、流体の流れの量に関する法則です。流体の質量流量は流線上のどの断面での常に一定であるということです。簡単に言えば、どこで切っても同じ量が流れているよということです。
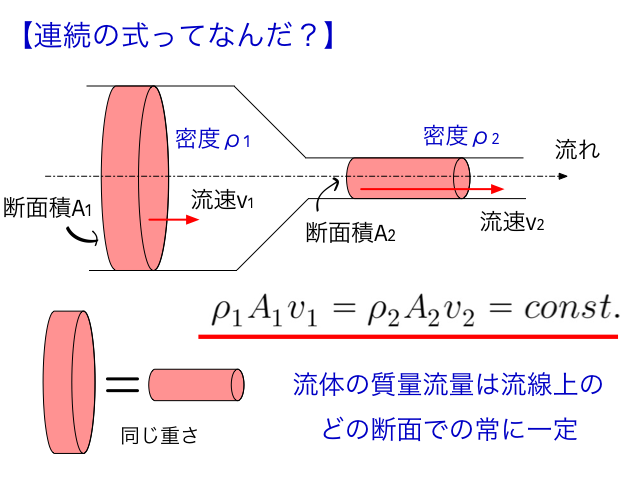
直観的には当たり前のような話なんですが、これがわかっていると任意の箇所の流速・流量・断面積などを計算して出すことができます。非常に便利な定理です。
簡単な演習問題を解いて理解を深めましょう。

まず、ρ1=ρ2のため連続の式はこのようにシンプルになります。
$$A_1 V_1=A_2 V_2 =const. $$
求めたいのはA2なので、式を変形して数字を代入します。
$$A_2=\frac{V_1}{V_2}\ A_1 =\frac{2}{6}\ 30= 10[mm^2]$$
となります。簡単ですね。
ベルヌーイの定理
ベルヌーイの定理は流体の流れのエネルギーに関する定理です。流体内のエネルギーの和が流線上で常に一定であるという定理です。流れる流体が持っているエネルギーは
・圧力エネルギー
・運動エネルギー
・位置エネルギー
の三つがあります。 この三つの合計は、どこの箇所でも一定だというのが、ベルヌーイの定理です。 中学の理科で習うエネルギー保存の法則の流体バージョンといった感じですね。
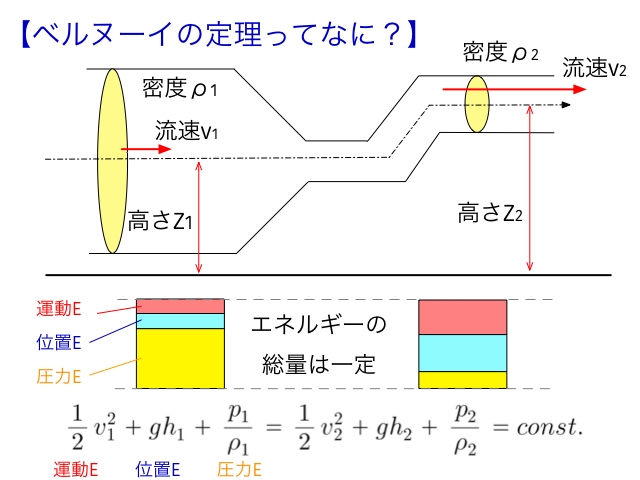
例えば
流れの圧力が上がれば速度は低下し、圧力が下がれば速度は上昇する 。
といった具合ですね。ベルヌーイの定理を知っていると任意の流れの流速・圧力・位置などを計算して出すことができます。さらには連続の式と組み合わせて、色々な流れの計算をすることができるんです。
簡単な演習問題を解いて理解を深めましょう。
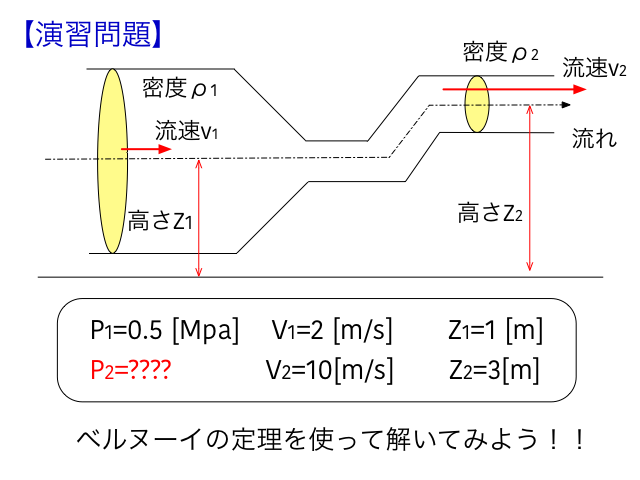
求めたいのはP2なので、式を変形します。
$$P_2=P_1+\frac{1}{2}\ \rho V_1^2+ \rho gz_1-\frac{1}{2}\ \rho V_2^2- \rho gz_2$$
後は、この式に数字を代入していきましょう。 式が長くなるので詳細は省きますが、4.3Mpaになるはずです。計算時には、単位の取り扱いには注意しましょう。
【ちょっと補足】
誤解の無いように補足すると、ベルヌーイの式は理想流体の条件で成り立ちます。理想流体とは、粘性のない究極にサラサラした液体のことで、流れるときに全く抵抗が発生しません。厳密に色々考え出すとキリがないから、とりあえず抵抗とか無視して考えましょうということですね。 また、上述の式は非圧縮性流体の式です。非圧縮性流体は、その名の通り圧縮することのできない流体です。水や油などの液体ですね。 空気の場合は、厳密にいえば圧縮流体用のベルヌーイの式で考える必要があるのですが、ちょっとややこしいので省略しました。圧縮流体の場合は、圧縮性を考慮する必要があるんです。詳しく知りたい人は、他ブログの記事ですがこの記事にわかりやすい解説がありますよ。
まとめ
本記事の復習をしましょう。
・圧力にはゲージ圧と絶対圧がある
・ボイル・シャルルの法則は、気体の温度・体積・圧力の関係を表した式です。
・パスカルの原理は、密閉された容器内の圧力はどこでも一定だという定理
・連続の式は、流体の流れの量に関する定理
・ベルヌーイの定理は、流体の流れのエネルギーに関する定理
さて、ここで冒頭の質問を振り返りましょう。

・絶対圧とゲージ圧の違いって何?
・ボイルシャルルの法則って、どういう法則?
・パスカルの原理って、どういうこと?
・連続の法則の意味を説明できる?
・ベルヌーイの定理ってどんな定理?
イメージしてください。友達、家族、または恋人があなたに、上記のような質問を投げかけてきたとします。 今のあなたはその質問に対して、どう説明しますか?頭の中で想像して答えてみましょう。もし説明がうまくできなかった部分があれば、それはあなたがまだ理解できていない部分ですよ。
正直な話、これらの理論を知らなくても機械を設計することはできます。もちろん使うことも然りです。しかし理論や法則を知っているのと、そうでないのでは雲泥の差があります。ものづくりのセンスは物理現象を正しく理解して、初めて身につくものなんです。その第一歩がこのような理論や法則に触れるということだと思います。技術者であれば、物理現象の理解を大切にしましょう。厳密に理解しようと思ったら、果てしないですが、その数式がどういう意味を持っていてどのように導出されたのか、というところまでは突っ込んで理解すると良いでしょう。
本記事で私が説明したのは、浅瀬も浅瀬です。理論の世界を大海原で例えるなら、まだ海にも入っていません。海の家についたくらいの話です。興味があれば、色々な参考書を買って突っ込んで勉強してみてくださいね。式を意味として理解できる技術者になりましょう!!
空気圧について、体系的にガッツリ勉強したいという方は下記の書籍がオススメです。